Post

R 시계열 분석

Posted
By 23 min read

시계열 분석(time series)은 계량 금융학과 증권 자동거래가 유망해짐에 따라 중요한 화두가 되었다. 그래서 이번에 다루는 기능들 중에는 금융, 증권거래, 자산관리 분야의 전문가 및 연구자들이 개발한 것이 다수 있다.

R에서 시계열 분석을 하기에 앞서, 결정해야 할 중요한 사항은 데이터 표현 방식(객체의 클래스)이다. R과 같은 객체 지향적 언어에서 특히 중요시되는 부분인데, 단순히 데이터가 저장되는 방식 이상의 영향을 미치기 때문이다. 클래스는 어떤 함수(메서드)로 데이터를 로딩하고, 처리하고, 분석하고, 출력하고, 그래프로 그릴수 있는지까지 좌우한다. 다들 처음 R을 사용할 때는 시계열 데이터를 단순하게 벡터에 저장하곤 한다. 그때는 벡터가 자연스러워보이기 때문이다. 하지만 곧, 단순 벡터로는 멋진 시계열 분석 방법을 사용할 수 없다는 사실을 알게 된다. 이후 사용자들이 시계을 분석을 위해 만들어진 객체 클래스로 바꾸어 사용하기 시작하면, 그제야 비로소 중요한 함수들과 분석 방법들에 입문하게 되곤 한다.

1
2
3
4
5
6
7
8
9
10

# 라이브러리 로드
library(tidyverse) # metapackage of all tidyverse packages

# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory

list.files(path = "../input")
org_df <- read_csv("/kaggle/input/kospi-20240308-csv/kospi_20240308.csv", show_col_types = FALSE)
tail(org_df)


1
2
3
4
5
6
7
8
9
10

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.4.4     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.0
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

‘kospi-20240308-csv’

A tibble: 6 × 6
dateopen_pricehigh_pricelow_pricetrade_pricevolume
<date><dbl><dbl><dbl><dbl><dbl>
2024-02-292643.482647.562628.622642.36496064469
2024-03-042664.522682.802662.322674.27404014324
2024-03-052660.802684.832649.352649.40457237152
2024-03-062638.842649.782630.162641.49378993989
2024-03-072653.982660.262633.572647.62462910823
2024-03-082676.792688.002668.382677.22435697586

이번장에서는 본격적으로 코스피 데이터셋(일별 기준)을 사용하여 시계열 데이터를 로딩하고, 처리하고, 분석하는 과정을 진행해보고자 한다.

  1. 시계열 데이터 표현하기

문제 : 시계열 데이터를 표현할 수 있는 R 데이터 구조를 찾고 싶다.

해결책 : zoo와 xts패키지를 추천한다. 이 패키지들은 시계을 분석을 위한 데이터 구조를 정의해 주며, 시계열 분석을 하는 데 유용한 함수도 많이 포함하고 있다. 다음과 같이 zoo 객체를 생성하면 된다. 여기서 x는 벡터, 행렬, 또는 데이터 프레임이고, dt는 이에 상응하는 날짜 또는 날짜시간으로 이루어진 벡터이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# Function to set Height & Width
fig<-function(x,y){
    options(repr.plot.width = x, repr.plot.height = y)
    }

fig(12,8)


library(zoo)
df <- org_df
# zoo 객체 생성: date를 인덱스로, trade_price를 데이터로 사용
# x : 종가
# dt : 날짜
x = df$trade_price
dt = df$date
ts <- zoo(x, order.by=dt)
print(ts)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

2023-05-15 2023-05-16 2023-05-17 2023-05-18 2023-05-19 2023-05-22 2023-05-23 
   2479.35    2480.24    2494.66    2515.40    2537.79    2557.08    2567.55 
2023-05-24 2023-05-25 2023-05-26 2023-05-30 2023-05-31 2023-06-01 2023-06-02 
   2567.45    2554.69    2558.81    2585.52    2577.12    2569.17    2601.36 
2023-06-05 2023-06-07 2023-06-08 2023-06-09 2023-06-12 2023-06-13 2023-06-14 
   2615.41    2615.60    2610.85    2641.16    2629.35    2637.95    2619.08 
2023-06-15 2023-06-16 2023-06-19 2023-06-20 2023-06-21 2023-06-22 2023-06-23 
   2608.54    2625.79    2609.50    2604.91    2582.63    2593.70    2570.10 
2023-06-26 2023-06-27 2023-06-28 2023-06-29 2023-06-30 2023-07-03 2023-07-04 
   2582.20    2581.39    2564.19    2550.02    2564.28    2602.47    2593.31 
2023-07-05 2023-07-06 2023-07-07 2023-07-10 2023-07-11 2023-07-12 2023-07-13 
   2579.00    2556.29    2526.71    2520.70    2562.49    2574.72    2591.23 
2023-07-14 2023-07-17 2023-07-18 2023-07-19 2023-07-20 2023-07-21 2023-07-24 
   2628.30    2619.00    2607.62    2608.24    2600.23    2609.76    2628.53 
2023-07-25 2023-07-26 2023-07-27 2023-07-28 2023-07-31 2023-08-01 2023-08-02 
   2636.46    2592.36    2603.81    2608.32    2632.58    2667.07    2616.47 
2023-08-03 2023-08-04 2023-08-07 2023-08-08 2023-08-09 2023-08-10 2023-08-11 
   2605.39    2602.80    2580.71    2573.98    2605.12    2601.56    2591.26 
2023-08-14 2023-08-16 2023-08-17 2023-08-18 2023-08-21 2023-08-22 2023-08-23 
   2570.87    2525.64    2519.85    2504.50    2508.80    2515.74    2505.50 
2023-08-24 2023-08-25 2023-08-28 2023-08-29 2023-08-30 2023-08-31 2023-09-01 
   2537.68    2519.14    2543.41    2552.16    2561.22    2556.27    2563.71 
2023-09-04 2023-09-05 2023-09-06 2023-09-07 2023-09-08 2023-09-11 2023-09-12 
   2584.55    2582.18    2563.34    2548.26    2547.68    2556.88    2536.58 
2023-09-13 2023-09-14 2023-09-15 2023-09-18 2023-09-19 2023-09-20 2023-09-21 
   2534.70    2572.89    2601.28    2574.72    2559.21    2559.74    2514.97 
2023-09-22 2023-09-25 2023-09-26 2023-09-27 2023-10-04 2023-10-05 2023-10-06 
   2508.13    2495.76    2462.97    2465.07    2405.69    2403.60    2408.73 
2023-10-10 2023-10-11 2023-10-12 2023-10-13 2023-10-16 2023-10-17 2023-10-18 
   2402.58    2450.08    2479.82    2456.15    2436.24    2460.17    2462.60 
2023-10-19 2023-10-20 2023-10-23 2023-10-24 2023-10-25 2023-10-26 2023-10-27 
   2415.80    2375.00    2357.02    2383.51    2363.17    2299.08    2302.81 
2023-10-30 2023-10-31 2023-11-01 2023-11-02 2023-11-03 2023-11-06 2023-11-07 
   2310.55    2277.99    2301.56    2343.12    2368.34    2502.37    2443.96 
2023-11-08 2023-11-09 2023-11-10 2023-11-13 2023-11-14 2023-11-15 2023-11-16 
   2421.62    2427.08    2409.66    2403.76    2433.25    2486.67    2488.18 
2023-11-17 2023-11-20 2023-11-21 2023-11-22 2023-11-23 2023-11-24 2023-11-27 
   2469.85    2491.20    2510.42    2511.70    2514.96    2496.63    2495.66 
2023-11-28 2023-11-29 2023-11-30 2023-12-01 2023-12-04 2023-12-05 2023-12-06 
   2521.76    2519.81    2535.29    2505.01    2514.95    2494.28    2495.38 
2023-12-07 2023-12-08 2023-12-11 2023-12-12 2023-12-13 2023-12-14 2023-12-15 
   2492.07    2517.85    2525.36    2535.27    2510.66    2544.18    2563.56 
2023-12-18 2023-12-19 2023-12-20 2023-12-21 2023-12-22 2023-12-26 2023-12-27 
   2566.86    2568.55    2614.30    2600.02    2599.51    2602.59    2613.50 
2023-12-28 2024-01-02 2024-01-03 2024-01-04 2024-01-05 2024-01-08 2024-01-09 
   2655.28    2669.81    2607.31    2587.02    2578.08    2567.82    2561.24 
2024-01-10 2024-01-11 2024-01-12 2024-01-15 2024-01-16 2024-01-17 2024-01-18 
   2541.98    2540.27    2525.05    2525.99    2497.59    2435.90    2440.04 
2024-01-19 2024-01-22 2024-01-23 2024-01-24 2024-01-25 2024-01-26 2024-01-29 
   2472.74    2464.35    2478.61    2469.69    2470.34    2478.56    2500.65 
2024-01-30 2024-01-31 2024-02-01 2024-02-02 2024-02-05 2024-02-06 2024-02-07 
   2498.81    2497.09    2542.46    2615.31    2591.31    2576.20    2609.58 
2024-02-08 2024-02-13 2024-02-14 2024-02-15 2024-02-16 2024-02-19 2024-02-20 
   2620.32    2649.64    2620.42    2613.80    2648.76    2680.26    2657.79 
2024-02-21 2024-02-22 2024-02-23 2024-02-26 2024-02-27 2024-02-28 2024-02-29 
   2653.31    2664.27    2667.70    2647.08    2625.05    2652.29    2642.36 
2024-03-04 2024-03-05 2024-03-06 2024-03-07 2024-03-08 
   2674.27    2649.40    2641.49    2647.62    2677.22

xts 함수도 비슷하게 xts 객체를 반환한다.

1
2
3

library(xts)
ts <- xts(x, order.by=dt)
print(ts)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

           trade_price high_price
2023-05-15     2479.35    2479.35
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40
2023-05-19     2537.79    2538.31
2023-05-22     2557.08    2564.09
2023-05-23     2567.55    2577.32
2023-05-24     2567.45    2572.21
2023-05-25     2554.69    2575.05
2023-05-26     2558.81    2567.50
       ...                       
2024-02-23     2667.70    2694.80
2024-02-26     2647.08    2659.60
2024-02-27     2625.05    2654.76
2024-02-28     2652.29    2657.32
2024-02-29     2642.36    2647.56
2024-03-04     2674.27    2682.80
2024-03-05     2649.40    2684.83
2024-03-06     2641.49    2649.78
2024-03-07     2647.62    2660.26
2024-03-08     2677.22    2688.00
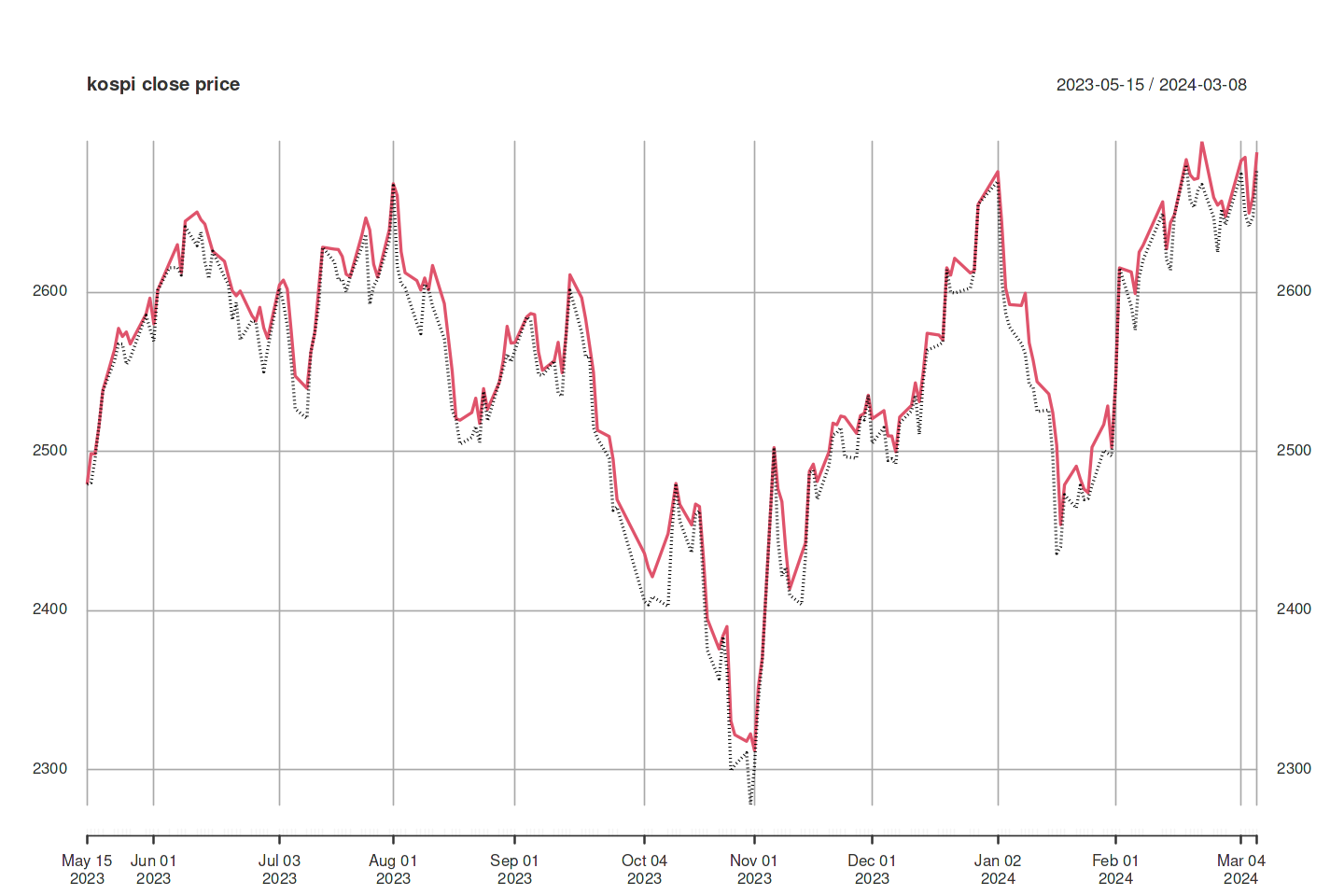
  1. 시계열 데이터로 그래프 그리기

문제 : 하나 또는 그 이상의 시계열을 그래프로 그리고 싶다.

해결책 : 하나 또는 여러개의 시계열을 담고 있는 zoo와 xts 객체에 모두 작동하는 plot(x)를 사용한다. 시계열 관찰이 담긴 단순 벡터 v에는 plot(v, type =”l”) 또는 plot.ts(v)를 쓰면 된다.

1
2
3
4
5
6
7
8
9
10

main <- "kospi close price"
lty <- c("dotted", "solid")


x = df[c("trade_price","high_price")]
dt = df$date
ts <- xts(x, order.by=dt)

plot(ts,
    lty = lty, main = main)

png

  1. 가장 오래전 또는 가장 최근 관찰 추출하기

문제 : 시계열에서 가장 오래전 또는 가장 최근 관찰만 보고 싶다.

해결책 : head를 사용해서 가장 오래된 관찰들을 찾는다. tail을 사용해서 가장 최근 관찰들을 찾는다.

1

head(ts)

1
2
3
4
5
6
7

           trade_price high_price
2023-05-15     2479.35    2479.35
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40
2023-05-19     2537.79    2538.31
2023-05-22     2557.08    2564.09

1

tail(ts)

1
2
3
4
5
6
7

           trade_price high_price
2024-02-29     2642.36    2647.56
2024-03-04     2674.27    2682.80
2024-03-05     2649.40    2684.83
2024-03-06     2641.49    2649.78
2024-03-07     2647.62    2660.26
2024-03-08     2677.22    2688.00

head와 tail은 기본 설정으로 각각 여섯 개의 가장 오래된 데이터와 가장 최근 데이터를 보여준다. tail(ts,20)처럼 둘째 인자에 값을 넣으면 더 많은 관찰을 볼 수 있다. xts 패키지에는 관찰의 개수 대신에 달력 기준 기간을 사용할 수 있는 first와 last 함수도 들어 있다. first와 last함수를 사용하면 일, 주, 월, 연도의 수를 기준으로 데이터를 선택할 수 있다.

1

first(ts, "2 week")

1
2
3
4
5
6
7
8
9
10
11

           trade_price high_price
2023-05-15     2479.35    2479.35
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40
2023-05-19     2537.79    2538.31
2023-05-22     2557.08    2564.09
2023-05-23     2567.55    2577.32
2023-05-24     2567.45    2572.21
2023-05-25     2554.69    2575.05
2023-05-26     2558.81    2567.50

3. 시계열 부분집합 만들기

문제: 어떤 시계열에서 하나 또는 그 이상의 원소를 선택하고 싶다.

해결책 : 다중 시계열인지에 따라 하나 혹은 두 개의 첨자를 사용하면 된다.

1
2

# xts객체에서 2~4번째 까지의 관찰 출력
ts[2:4]

1
2
3
4

           trade_price high_price
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40

1
2

# xts 객체에서 2023년 5월 16일의 관찰 출력
ts[as.Date("2023-05-16")]

1
2

           trade_price high_price
2023-05-16     2480.24    2498.54

1
2

# 연이은 날짜 범위를 선택할 때는 window 함수가 더 편하다.
window(ts, start=as.Date("2023-05-16"), end=as.Date("2023-05-30"))

1
2
3
4
5
6
7
8
9
10
11

           trade_price high_price
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40
2023-05-19     2537.79    2538.31
2023-05-22     2557.08    2564.09
2023-05-23     2567.55    2577.32
2023-05-24     2567.45    2572.21
2023-05-25     2554.69    2575.05
2023-05-26     2558.81    2567.50
2023-05-30     2585.52    2586.22

4. 시계열 늦추기

문제 : 시계열의 시간을 앞으로 또는 뒤로 옮기고 싶다.

해결책 : lag 또는 lead 함수를 사용한다.

1
2
3
4
5
6

sub_ts <- ts[2:10]
print(sub_ts)

#날짜를 하루 앞으로 옮겨 데이터를 당기려면 k = +1을 사용한다.
lag(sub_ts)
lead(sub_ts)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

           trade_price high_price
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40
2023-05-19     2537.79    2538.31
2023-05-22     2557.08    2564.09
2023-05-23     2567.55    2577.32
2023-05-24     2567.45    2572.21
2023-05-25     2554.69    2575.05
2023-05-26     2558.81    2567.50



           trade_price high_price
2023-05-16          NA         NA
2023-05-17     2480.24    2498.54
2023-05-18     2494.66    2498.37
2023-05-19     2515.40    2515.40
2023-05-22     2537.79    2538.31
2023-05-23     2557.08    2564.09
2023-05-24     2567.55    2577.32
2023-05-25     2567.45    2572.21
2023-05-26     2554.69    2575.05



           trade_price high_price
2023-05-16     2494.66    2498.37
2023-05-17     2515.40    2515.40
2023-05-18     2537.79    2538.31
2023-05-19     2557.08    2564.09
2023-05-22     2567.55    2577.32
2023-05-23     2567.45    2572.21
2023-05-24     2554.69    2575.05
2023-05-25     2558.81    2567.50
2023-05-26          NA         NA

5. 연속차분 계산하기

문제 : 시계열 x가 주어졌을 때 연속된 관찰들 사이의 차이를 계산하고 싶다. (x2-x1), (x3-x2), (x4-x3)

해결책 : diff 함수를 사용한다.

1
2
3
4
5
6
7
8

sub_ts <- ts[2:10]
print(sub_ts)

# 2023년 5월 16일의 변화량을 계산할 수 없기 때문에, 차분된 시계열은 원래의 시계열보다 원소 하나가 짧다. 
diff(sub_ts)

# lag 매개변수를 사용하면 좀 더 넓은 간격으로 된 차분을 계산할 수 있다.
diff(sub_ts, lag=3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

           trade_price high_price
2023-05-16     2480.24    2498.54
2023-05-17     2494.66    2498.37
2023-05-18     2515.40    2515.40
2023-05-19     2537.79    2538.31
2023-05-22     2557.08    2564.09
2023-05-23     2567.55    2577.32
2023-05-24     2567.45    2572.21
2023-05-25     2554.69    2575.05
2023-05-26     2558.81    2567.50



           trade_price high_price
2023-05-16          NA         NA
2023-05-17       14.42      -0.17
2023-05-18       20.74      17.03
2023-05-19       22.39      22.91
2023-05-22       19.29      25.78
2023-05-23       10.47      13.23
2023-05-24       -0.10      -5.11
2023-05-25      -12.76       2.84
2023-05-26        4.12      -7.55



           trade_price high_price
2023-05-16          NA         NA
2023-05-17          NA         NA
2023-05-18          NA         NA
2023-05-19       57.55      39.77
2023-05-22       62.42      65.72
2023-05-23       52.15      61.92
2023-05-24       29.66      33.90
2023-05-25       -2.39      10.96
2023-05-26       -8.74      -9.82

6. 시계열 데이터 계산 수행하기

문제 : 시계열 데이터에 산술 연산 및 일반적인 함수를 사용하고 싶다.

해결책 : 문제없다. R은 zoo 및 xts 객체 연산을 아주 잘 수행한다. 산술 연산(+,-,*,/ 등) 뿐만 아니라 일반적인 함수(sqrt, log 등)도 사용할 수 있으며, 대개의 경우 원하는 결과를 얻을 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12

x = df[c("trade_price")]
dt = df$date
ts <- xts(x, order.by=dt)
sub_ts <- ts[2:10]

#코스피 지수에서 퍼센트 변화량을 계산하고 싶다고 해보자. 일일 변화량을 종가로 나눠야 하지만, 그 두가지 시계열은 자동으로 줄이 맞춰져 있지 않다. 시작 시간도 다르고, 길이도 다르기 때문이다.
# 다행히도 R은 똑똑하게 해당 시계열들의 줄을 맞추고 xts 객체를 반환해준다.
rate_of_change <- diff(sub_ts) / sub_ts[-1]
print(rate_of_change)

updated_sub_ts <- merge(sub_ts, rate_of_change = rate_of_change)
print(updated_sub_ts)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

             trade_price
2023-05-17  5.780347e-03
2023-05-18  8.245210e-03
2023-05-19  8.822637e-03
2023-05-22  7.543761e-03
2023-05-23  4.077817e-03
2023-05-24 -3.894915e-05
2023-05-25 -4.994735e-03
2023-05-26  1.610123e-03
           trade_price trade_price.1
2023-05-16     2480.24            NA
2023-05-17     2494.66  5.780347e-03
2023-05-18     2515.40  8.245210e-03
2023-05-19     2537.79  8.822637e-03
2023-05-22     2557.08  7.543761e-03
2023-05-23     2567.55  4.077817e-03
2023-05-24     2567.45 -3.894915e-05
2023-05-25     2554.69 -4.994735e-03
2023-05-26     2558.81  1.610123e-03

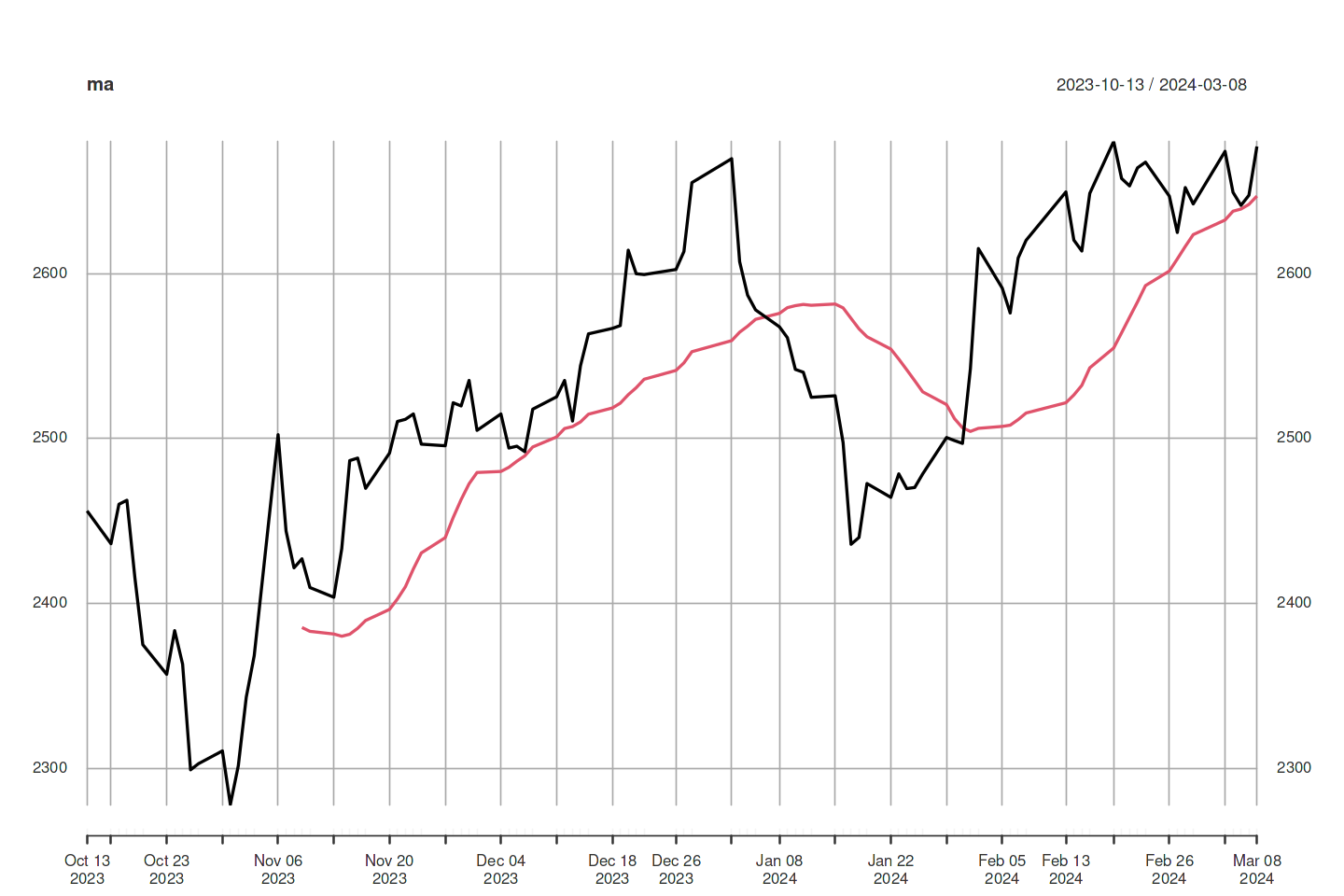
7. 이동평균 계산하기

문제 : 어떤 시계열의 이동편균을 계산하고 싶다.

해결책 : zoo 패키지의 rollmean 함수를 사용해서 ‘k-기간’의 이동평균을 구한다.

1
2
3
4
5
6
7
8
9

x = df[c("trade_price")]
dt = df$date
ts <- xts(x, order.by=dt)

sub_ts <- last(ts,100)
ma <-rollmean(sub_ts, 20, align="right")
ma <- merge(sub_ts, ma)
tail(ma)
plot(ma)

1
2
3
4
5
6
7

           trade_price trade_price.1
2024-02-29     2642.36      2623.750
2024-03-04     2674.27      2632.609
2024-03-05     2649.40      2637.956
2024-03-06     2641.49      2639.265
2024-03-07     2647.62      2642.081
2024-03-08     2677.22      2647.131

png

7. 달력 주기로 함수 적용하기

문제 : 주어진 시계열의 달력 주기(예 : 주, 월 또는 연도)를 가지고 데이터를 집단으로 나눈 다음, 각 집단에 함수를 적용해보고 싶다.

해결책 : xts 패키지에는 시계열을 일, 주, 월, 분기 또는 연도로 처리할 수 있는 함수들이 들어 있다.

  • apply.daily(ts, f)
  • apply.weekly(ts, f)
  • apply.monthly(ts, f)
  • apply.quarterly(ts, f)
  • apply.yearly(ts, f)

여기서 ts는 xts 시계열이고, f는 각 일, 주, 월, 분기 또는 연도에 적용할 함수다.

1
2
3
4
5
6

#ts 객체는 일자단위로 코스피 종가가격이 저장되어 있다.
tail(ts)

# apply.monthly와 mean을 함께 사용하면 월별 평균 가격을 계산할 수 있다.
kospi_mm <- apply.monthly(ts, mean)
print(kospi_mm)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

           trade_price
2024-02-29     2642.36
2024-03-04     2674.27
2024-03-05     2649.40
2024-03-06     2641.49
2024-03-07     2647.62
2024-03-08     2677.22


           trade_price
2023-05-31    2539.638
2023-06-30    2598.913
2023-07-31    2594.387
2023-08-31    2562.052
2023-09-27    2543.822
2023-10-31    2392.136
2023-11-30    2458.948
2023-12-28    2553.641
2024-01-31    2518.588
2024-02-29    2630.416
2024-03-08    2658.000

1
2

# 월별 종가의 표준편차는 다음과 같이 계산한다.
apply.monthly(diff(log(ts)), sd)

1
2
3
4
5
6
7
8
9
10
11
12

           trade_price
2023-05-31          NA
2023-06-30 0.006391609
2023-07-31 0.008634964
2023-08-31 0.008567943
2023-09-27 0.008081934
2023-10-31 0.012797079
2023-11-30 0.015065360
2023-12-28 0.008132888
2024-01-31 0.008972812
2024-02-29 0.010975647
2024-03-08 0.009150892

8. ARIMA 모형 적합시키기

문제 : 시계열 데이터에 ARIMA 모형을 적합시키고 싶다.

해결책 : forecast 패키지에 들어있는 auto.arima 함수는, 데이터에 대해 올바른 모형 차수를 선택하고 모형을 적합시켜 준다.

3단계에 거쳐 ARIMA 모형을 생성할 수 있다.

  1. 모형의 차수를 식별한다.
  2. 계수를 주면서 모형을 데이터에 적합시킨다.
  3. 진단척도를 적용해서 모형을 입증한다.

모혐의 ‘차수(order)’는 대개 정수 세 개(p,d,q)인데, 여기서 p는 자기 상관계수의 개수이며 d는 차분의 정도, q는 이동평균계수의 개수다. ARIMA 모형을 만들 때는 처음엔 적당한 차수가 뭔지 전혀 모르는 경우가 많다. 그래수 우리는 p,q,d의 가장 좋은 조합을 지겹게 찾지 않고, 함수가 대신해서 찾아 주도록 auto.arima를 사용한다.

1
2
3
4
5
6
7
8
9

library(forecast)

x = df[c("trade_price")]
dt = df$date
ts <- xts(x, order.by=dt)
ma <-rollmean(ts, 20, align="right")
sub_ts <- last(ma,150)
print(sub_ts)
auto.arima(sub_ts)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

           trade_price
2023-07-27    2590.276
2023-07-28    2592.477
2023-07-31    2593.983
2023-08-01    2597.671
2023-08-02    2599.544
2023-08-03    2602.000
2023-08-04    2605.804
2023-08-07    2608.805
2023-08-08    2609.379
2023-08-09    2610.899
       ...            
2024-02-23    2592.829
2024-02-26    2601.666
2024-02-27    2608.991
2024-02-28    2616.573
2024-02-29    2623.750
2024-03-04    2632.609
2024-03-05    2637.956
2024-03-06    2639.265
2024-03-07    2642.081
2024-03-08    2647.132



Series: sub_ts 
ARIMA(1,2,1) 

Coefficients:
          ar1     ma1
      -0.5630  0.7319
s.e.   0.2153  0.1767

sigma^2 = 3.942:  log likelihood = -308.81
AIC=623.62   AICc=623.79   BIC=632.61

이 경우 auto.arima는 최선의 차수가 (1,2,1)이라고 결정했다. 해석해보면, AR 계수가 1개(p=1)와 MA 계수 한 개(q=2)가 있는 모형을 선택했고, 그 전에 데이터를 1번 차분(d=1)했다는 뜻이다.

1
2
3
4
5
6
7
8

# 위 결과를 바탕으로 arima 모델 생성
m <- arima(sub_ts, order = c(1, 2, 1))


confint(m)

m <- arima(sub_ts, order = c(1, 2, 1), fixed = c(0,NA))
confint(m)
A matrix: 2 × 2 of type dbl
2.5 %97.5 %
ar1-0.984850-0.141074
ma1 0.385485 1.078229
1
2

Warning message in arima(sub_ts, order = c(1, 2, 1), fixed = c(0, NA)):
“some AR parameters were fixed: setting transform.pars = FALSE”
A matrix: 2 × 2 of type dbl
2.5 %97.5 %
ar1 NA NA
ma1-0.01755610.3492272

9. ARIMA 모형 진단하기

문제 : forecast 패키지를 사용해서 ARIMA 모형을 만들었고, 이제 그 모형을 입증하기 위해서 진단 검정들을 실행하고 싶다.

해결책 : checkresiduals 함수를 사용한다. 다음 예시는 auto.arima를 사용해서 ARIMA 모형을 적합한 다음, m에 모형을 저장하고 실행한다.

1
2
3

m <- auto.arima(sub_ts)
tail(sub_ts)
checkresiduals(m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

           trade_price
2024-02-29    2623.750
2024-03-04    2632.609
2024-03-05    2637.956
2024-03-06    2639.265
2024-03-07    2642.081
2024-03-08    2647.132



	Ljung-Box test

data:  Residuals from ARIMA(1,2,1)
Q* = 3.724, df = 8, p-value = 0.8811

Model df: 2.   Total lags used: 10

png

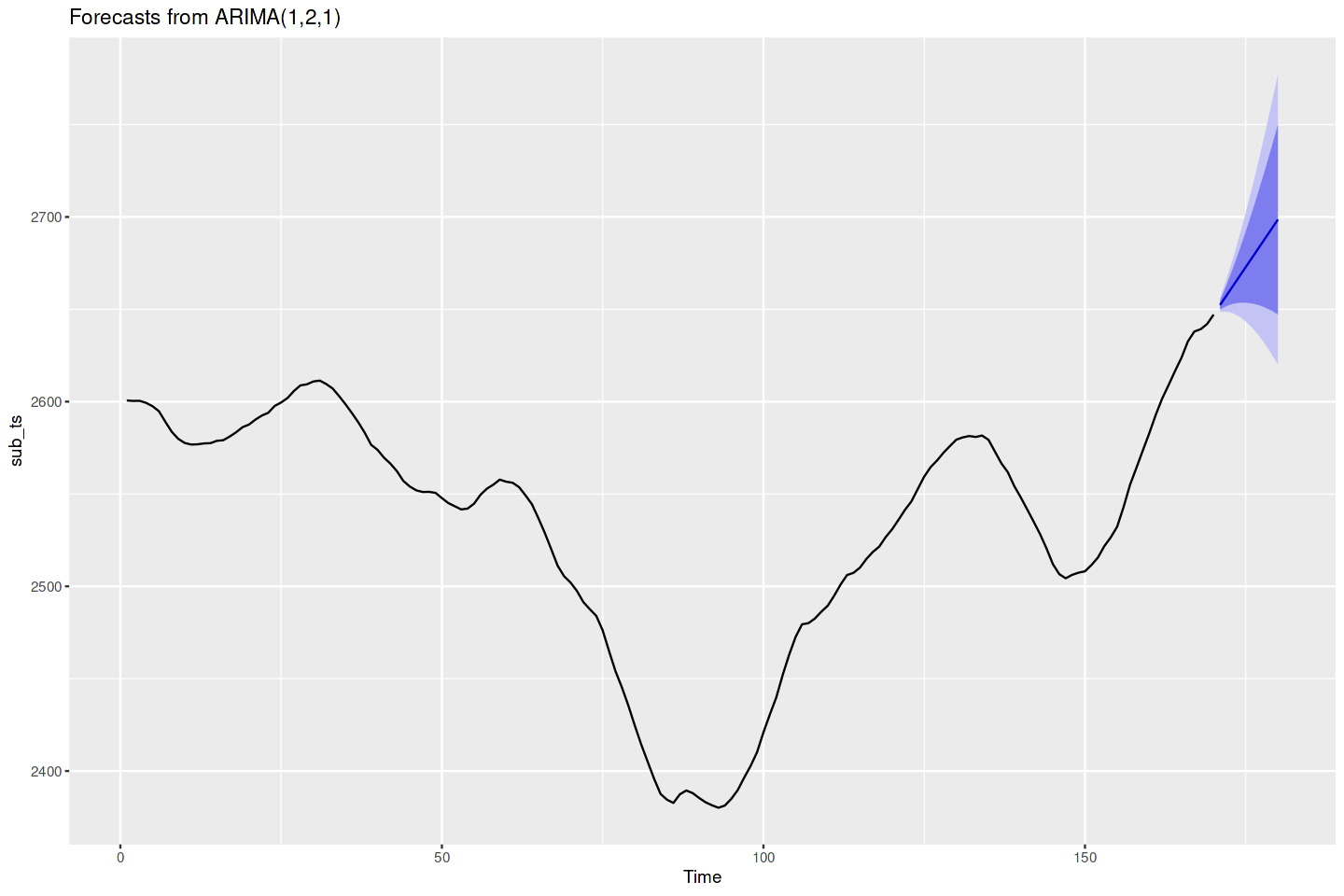
10. ARIMA 모형을 통해 예측하기

문제 : forecast 패키지를 사용해서 만든 시계열 데이터에 대한 ARIMA 모형이 있으며, 시계열에서 다음에 일어날 관찰 몇개를 예측하고 싶다.

해결책 :해당 모형을 객체에 저장한다. 그리고 forecast 함수를 객체에 적용한다.

1
2
3
4
5
6
7
8

x = df[c("trade_price")]
dt = df$date
ts <- xts(x, order.by=dt)
ma <-rollmean(ts, 20, align="right")
sub_ts <- last(ma,170)
m <- arima(sub_ts, order = c(1, 2, 1))
fc_m <- forecast(m)
autoplot(fc_m)

png

Blogging, R_tip
Statistics R_tip
This post is licensed under CC BY 4.0 by the author.